Catapults in Room 9

 Kia ora whānau,

Two scientific capabilities we have examined this year are observing and using evidence. These were explored during a class catapult challenge. Here group had to design catapults during only popsicle sticks, rubber bands and a cup to shot a pompom as far as possible. The class showed great resilience in their observations as they altered their designs to create the most elastic force possible. Evidence was collected using a trundle wheel and most groups were able to fire their pompom well over 4 metres!

Well done Room 9 – you are thinking like scientists!

Here is Christopher's catapult that he made at home – well done Christopher! I love the face and it looks like to have really used the elastics well to create more power.

Wet Lunchtimes in Room 9

Kia ora whānau,

It is so great to all be back at school! Unfortunately we have had a few rainy days since we have moved back to Level 2. Here is what members of Room 9 do on such days:

At-home Learning for Tuesday, September 7th

Kia ora Room 9,

I hope you are all well. 

I know it is not always easy to learn at home so thank you for being resilient and doing your best.

I really look forward to seeing you all on Thursday!

I have added the following tasks for today:

PĀNGARAU: Warm-up, Numbers of the Day and Maths Challenge (click on the “Pānagrau” tab above).

I have also added work to your modelling book (see the “Pānagrau L:inks”).

PĀNUI: I have added more slides to the inferencing activityand another literacy challenge: Who Stole the Emoji’s Colour?

PŪTAIAO:As you know, Hamilton East School is an Enviroschool.

Click on the “Pūtaiao” tab at the top of the blog for an Enviroschool challenge.

You can try at home. If you do this challenge, please share your results!

You can also try e-ako Maths. There are instructions below for how to register.

Greg

A Wee Challenge for Monday!

 

Our School Bubble

Hi everyone, 

Greg, Whaea Kat and I are at school in Room 8 and 9 with these lovely people. We are enjoying the spring sunshine. Can you see people from your class? We hope you are all having a lovely day and enjoying the home mahi that you are doing! We are having fun but looking forward to seeing you all when we are allowed to be back together again. Keep up your great online learning and enjoy the moments when you can get outside and go for a walk, ride, etc

Online learning

Card games

Our bubble teachers

The plum tree is blooming!

Time for some painting ....

And being scientists too!!

Numbers of the Day

 

Inferencing Activity

 

Pāngarau Answers

Einstein's Riddle

1. Emma lives in the first house. (#9) Emma lives next to the blue house. (#14) House #2 is blue.
2. The child in house #3 drinks milk. (#8) The child in the green house drinks lemonade. (#5) House #3 is not green.
3. The green house immediately comes before the white house. (#4) House #1 cannot be green. If house #1 were green, then house #2 would be white. However, house #2 is blue. House #2 cannot be green. It is already listed as blue. House #3 is already listed as not green. Therefore, house #4 must be green and house #5 must be white.
4. Peter lives in the red house. (#1) We already know that houses #2, #4, and #5 are blue, green, and white, so he does not live there. House #1 is Emma’s. The only one left is house #3.
5. We now know that houses #2, #3, #4, #5 are blue, red, green, and white. Therefore, house #1 is yellow.
6. The child in the yellow house likes chocolate. Therefore, Emma in house #1 likes chocolate.
7. The child who has a horse lives next to the child who likes chocolate. Emma, who likes chocolate, has only one neighbour. Therefore, the horse goes with house #2.
8. Mary has a dog. We already know the occupants of houses #1 and #3. House #2 already has a pet. Therefore, Mary lives in #4 or #5.
9. Linus drinks tea. We already know the occupants of houses #1 and #3 and the drinks of houses #3 and #4. Therefore, Linus lives in #2 or #5.
10. Anna likes cake. We already know the occupants of houses #1 and #3. Therefore, Anna lives in #2, #4, or #5.
11. The child who likes cookies has birds. Food nor pet are unknown for #3, #4, or #5.
12. The child who likes sweets lives next to the child who drinks water. Possible houses are #2, #3 or #4.
13. The child who likes gum drinks juice. Possible houses are #2 or #5.
14. The child who likes gum drinks juice. Anna and Emma’s food are known. Linus and Peter’s drink are known. Therefore, Mary likes gum and drinks juice. Juice and gum can go in #2 or #5. Mary can go in #4 or #5.#5 is the only common number. Therefore, Mary lives in house #5.
15. House #2 is the only house for which child AND drink are not known. Therefore, Linus lives in house #2.
16. Emma is the only child for whom drink is unknown. The only drink left is water.
17. Anna is the only child for whom housing is  unknown. The only house open is #4.
18. Cookies and birds go together. Peter, in house #3, is the only one for whom either is unknwon.
19. Sweets is the only food left. The only open slot for food is at house #2.
20. The child who likes sweets (House #2) has a neighbour with a cat. (#10) House #1 is the only neighbor with an open pet slot.
21. Anna has fish.

Adapted from https://www.mathnasium.com/redwood-city-san-carlos-news-einsteins-riddle

Short Maths Challenges

October 18:

You might disagree with me, but I think there are 30 squares:

1. There are 17 small RED squares (4 x 4 and 1 square in the middle).

2. There are 4 larger PINK squares (Imagine dividing the picture into quarters).

3. There are 4 even BLUE larger squares (These can be made by using 3 x 3 of the small squares).

4. There are 4 every small YELLOW squares (These are made with the small square in the middle).

5. There is 1 very large square (4 x 4 small squares).

The answer to the picture cube question is C.

Warm-ups

September 7:

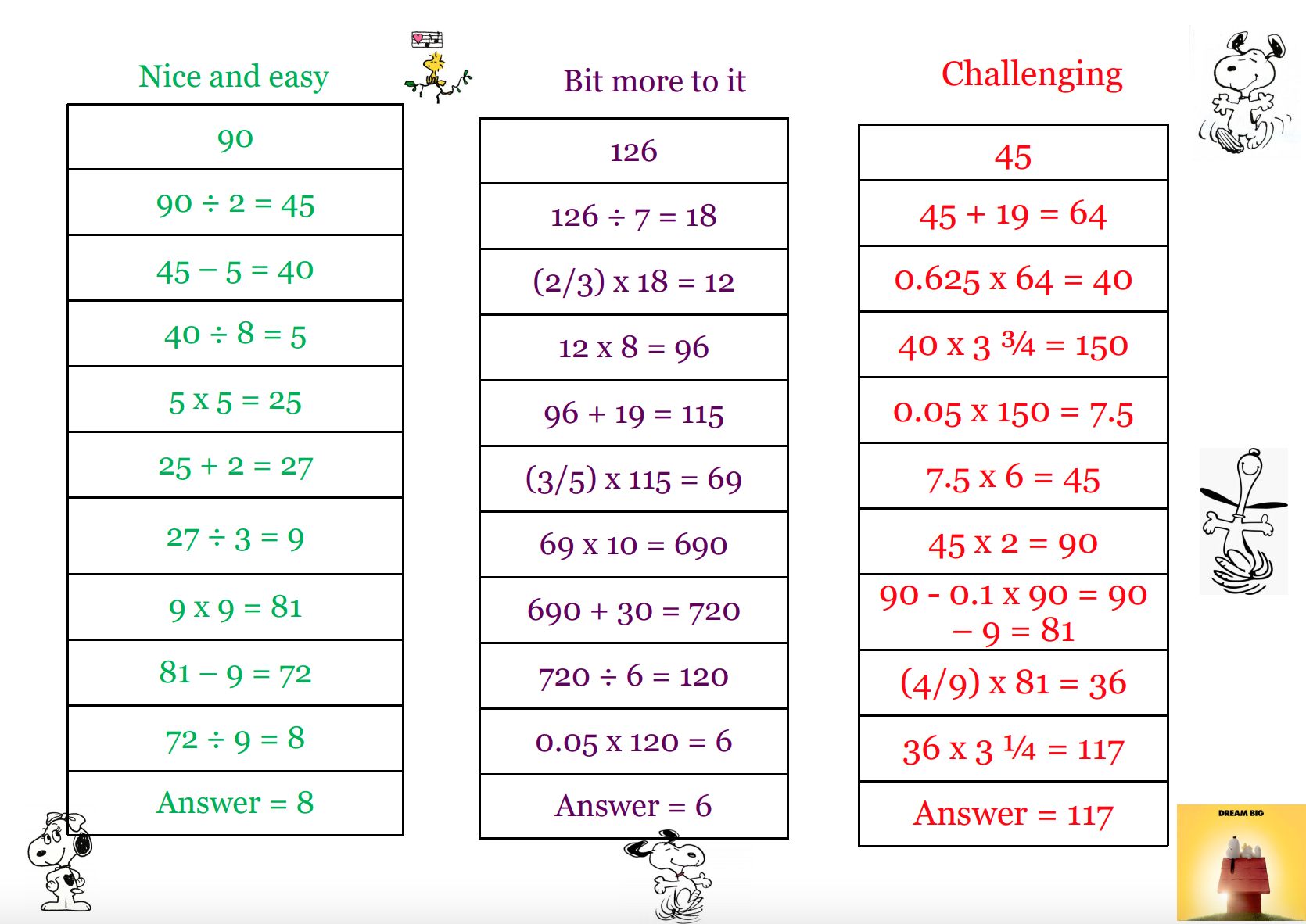
September 6:

September 3:

September 2:

August 31:

August 30:

Maths Challenges

September 7, Ball Problem

The bottom layer has 4 rows of 4 so 4 x 4 = 16.

The second layer has 3 rows of 3 so 3 x 3 = 9.

The third layer has 2 rows of 2 so 2 x 2 = 4.

There is 1 ball on top.

So 16 + 9 + 4 + 1 = 30. There are 30 balls.

September 6 Flower Problem

This can be solved with the equation 60 ÷3 = 20

We know the red flower is 20, so we can subtract that.

 This can be solved with the equation 10 ÷2 = 5

We know the blue flower is 5, so this means 5 – 2 = 3. The flowers are 2. So each yellow flower is 1.

Now we know the values of all of the flowers: 1 + 20 + 5 = 26

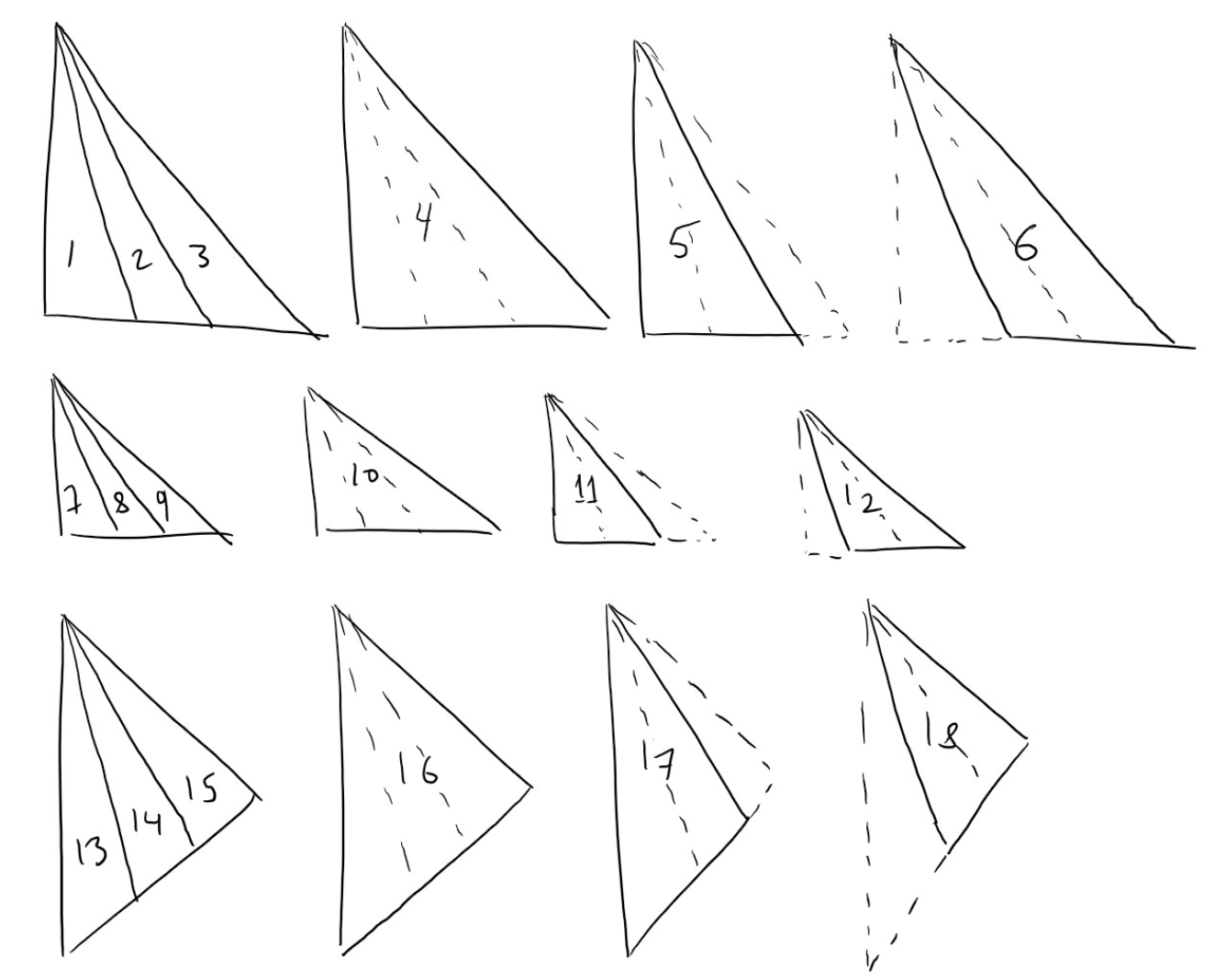
September 3, Triangles Problem

There are 24 triangles:

September 2, Blocks Problem

There are four arms in the block pattern. Each arm has 15 blocks and there are another 6 blocks in the centre. So the answer is (4 x 15) + 6 = 66 blocks. 

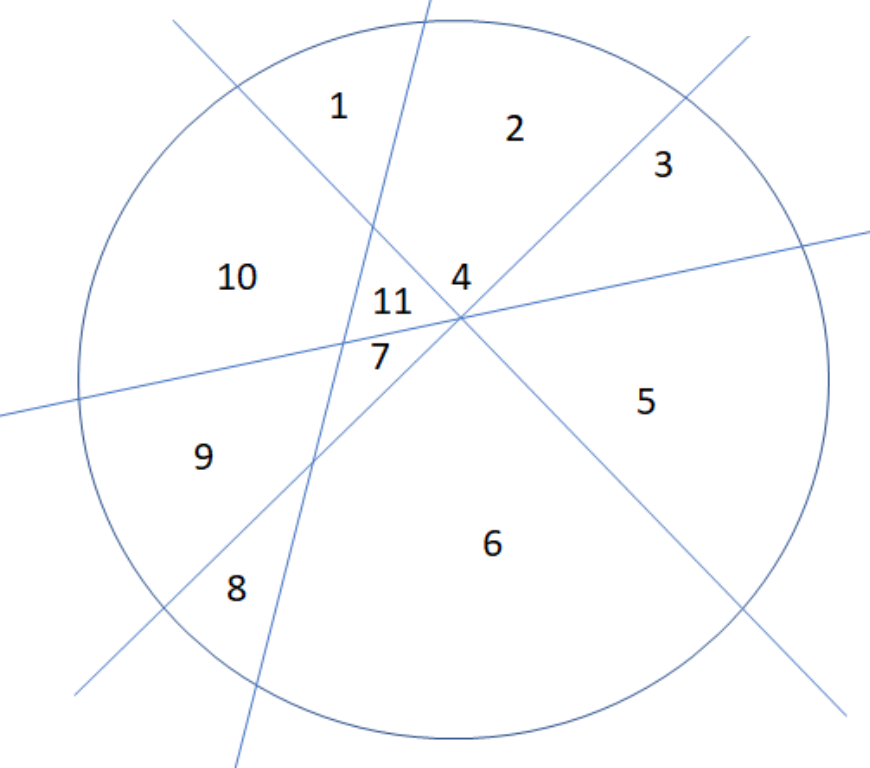
August 31, Pizza Problem

August 30, Roald Dahl Challenge 2:

The value of the characters is as follows: 

The Twits (older couple) are 5, 

George (boy) is 25, 

Willy Wonka (man with the cane) is 50, 

Enormous Crocodile is 10 

and Matilda (girl) is 30. 

August 27, Falling Origami Papers Problem Maths Challenge:

August 26, Roald Dahl Math Challenge 1:

Order of George’s bottles is as follows: Blue, Purple, Red, Green, Orange and Yellow.

 

 

 

Imposters

August 27:

The first imposter is blue (48 ÷ 8 = 6). Maybe you know this as a basic fact. 

The second imposter is orange (48 x 2 = 96). One strategy for this is to remember that 50 x 2 = 100. 50 – 48 = 2. We then subtract 2 x 2 from 100: 100 – 4 = 96.

The third imposter is dark grey (88 x 2 = 176). One strategy for this is to double 80 which is 160. Then double 8 which is 16. So 160 + 16 = 176.

The fourth imposter is brown (28 x 3 = 84). You can work this out by multiplying 20 by 3 which is 60. Then 8 x 3 = 24. 60 + 24 = 84.

August 26:

 

The first imposter is blue (66 ÷ 3 = 21). I worked this out 30 ÷ 3 = 10, so 60 ÷ 3 = 20. Then there are two more groups of 2 which means 20 + 2 = 21.

The second imposter is green (125 x ⅕ = 125, not 125 x ⅙). 

Here is some more instructions on how to multiple a whole number by a fraction:

August 25:

The first imposter is orange (126 ÷ 6 = 21). I worked this out 60 ÷ 6 = 10, so 120 ÷ 6 = 20. 

Then there is one more group of 6 which means 20 + 1 = 21.

The second imposter is brown (1234 + 5678 = 6912). I used column addition to calculate this:

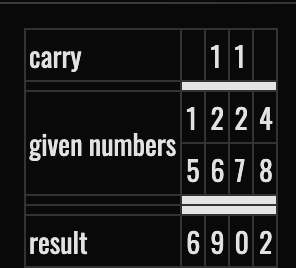
Every other equation was correct so there were only two imposters.

Numbers of the Day

Thursday, August 26

12

twelve; 

even; 

half it = 6; 

double it = 24; 

tens = 1, ones = 2; 

10 less = 2, 10 more = 22, 100 less = -88, 100 more = 112; 

add 15 = 27, subtract 7 = 5, multiply by 6 = 72, divide by 3 = 4; 

12 x 10 = 120, 12 x 100 = 1200, 12 ÷ 10 = 1.2, 12 ÷ 100 = 0.12  

Your number line example with 12 highlighted:

Number sentence (equation) example:

12 + 5 = 17

86

eighty-six; 

even; 

half it = 43; 

double it = 172; 

tens = 8, ones = 6; 

10 less = 86, 10 more = 96, 100 less = -14, 100 more = 186; 

add 15 = 101, subtract 7 = 79, multiply by 6 = 516, divide by 3 = 28 R2; 

86 x 10 = 860, 86 x 100 = 8600, 86 ÷ 10 = 8.6, 86 ÷ 100 = 0.86  

Your number line example with 86 highlighted:

 

Number sentence (equation) example:

81 + 5 = 86

972

nine-hundred and seventy-two; 

even; 

half it = 486; 

double it = 1944; 

hundreds = 9, tens = 7, ones = 2; 

10 less = 962, 10 more = 982, 100 less = 872, 100 more = 1072; 

add 15 = 987, subtract 7 = 965, multiply by 6 = 5,832 (I used the columns strategy), divide by 3 = 324 (I used long division); 

972 x 10 = 9,720; 972 x 100 = 97,200; 972 ÷ 10 = 97.2, 972 ÷ 100 = 9.72  

Your number line example with 972 highlighted:

 

Number sentence (equation) example:

972 + 5 = 977

5,762

five-thousand, seven-hundred and sixty-two; 

even; 

half it = 4,881; 

double it = 11,524; 

thousands = 5, hundreds = 7, tens = 6, ones = 2; 

10 less = 5,752, 10 more = 5,772, 100 less = 5,662, 100 more = 5,862; 

add 15 = 5,777; subtract 7 = 5,655; multiply by 6 = 34,572 (I used the columns strategy), divide by 3 = 1,920 R2 (I used long division); 

5,762 x 10 = 57,620; 5,762 x 100 = 576,200; 5,762 ÷ 10 = 576.2; 5,762 ÷ 100 = 57.62   

Your number line example with 5,762 highlighted:

Number sentence (equation) example:

5,762 + 5 = 5,767

Wednesday, August 25

10 (It doesn't hurt to do it again!)

ten; 

even; 

half it = 5; 

double it = 20; 

tens = 1, ones = 0; 

10 less = 0, 10 more = 20, 100 less = -90, 100 more = 110; 

add 15 = 25, subtract 7 = 3, multiply by 6 = 60, divide by 3 = 3 R1; 

10 x 10 = 100, 10 x 100 = 1,000, 10 ÷ 10 = 1, 10 ÷ 100 = 0.1   

Your number line example with 10 highlighted:

 

Number sentence (equation) example:

10 + 5 = 15

20

twenty; 

even; 

half it = 10; 

double it = 40; 

tens = 2, ones = 0; 

10 less = 10, 10 more = 30, 100 less = -80, 100 more = 120; 

add 15 = 35, subtract 7 = 13, multiply by 6 = 120, divide by 6 = 3 R2; 

20 x 10 = 200, 20 x 100 = 2,000, 20 ÷ 10 = 2, 20 ÷ 100 = 0.2   

Your number line example with 20 highlighted:

Number sentence (equation) example:

20 + 5 = 25

67

sixty-seven; 

odd; 

half it = 33.5; 

double it = 134; 

tens = 6, ones = 7; 

10 less = 57, 10 more = 77, 100 less = -33, 100 more = 167; 

add 15 = 82, subtract 7 = 60, multiply by 6 = 402, divide by 3 = 22 R1; 

67 x 10 = 670, 67 x 100 = 6,700, 67 ÷ 10 = 6.7, 81 ÷ 100 = 0.67   

Your number line example with 8 highlighted:

 

Number sentence (equation) example:

67 + 5 = 72

928

nine-hundred and twenty-eight; 

even; 

half it = 464; 

double it = 1,856; 

hundreds = 9, tens = 2, ones = 8; 

10 less = 918, 10 more = 938, 100 less = 828, 100 more = 1,028; 

add 15 = 942, subtract 7 = 921, multiply by 6 = 5,568 (I used the columns strategy), divide by 3 = 309 R1 (I used long division); 

928 x 10 = 9,280; 928 x 100 = 92,800; 928 ÷ 10 = 92.8, 928 ÷ 100 = 9.28   

Your number line example with 928 highlighted:

Number sentence (equation) example:

928 + 5 = 933

4,632

four-thousand, six-hundred and thirty-two; 

even; 

half it = 2,616; 

double it = 9,264; 

thousands = 4, hundreds = 6, tens = 3, ones = 2; 

10 less = 4,622, 10 more = 4,642, 100 less = 4,532, 100 more = 4,732; 

add 15 = 4,647; subtract 7 = 4,625; multiply by 6 = 27,792 (I used the columns strategy), divide by 3 = 1,544 (I used long division); 

4,632 x 10 = 46,320; 4,632 x 100 = 463,200; 4,632 ÷ 10 = 463.2; 4,632 ÷ 100 = 46.32   

Your number line example with 4,632 highlighted:

Number sentence (equation) example:

4,632 + 5 = 4,637

Tuesday, August 24

5

five; 

odd; 

half it = 2.5; 

double it = 10; 

tens = 0, ones = 5; 

10 less = -5, 10 more = 15, 100 less = -95, 100 more = 105; 

add 15 = 20, subtract 7 = -2, multiply by 6 = 30, divide by 3 = 1 R2; 

5 x 10 = 50, 5 x 100 = 500, 5 ÷ 10 = 0.5, 5 ÷ 100 = 0.05   

Your number line example with 5 highlighted:

 

Number sentence (equation) example:

5+ 5 = 10

81

eighty-one; 

odd; 

half it = 40.5; 

double it = 162; 

tens = 8, ones = 1; 

10 less = 71, 10 more = 91, 100 less = -19, 100 more = 181; 

add 15 = 96, subtract 7 = 74, multiply by 6 = 486, divide by 3 = 27; 

81 x 10 = 810, 81 x 100 = 8100, 81 ÷ 10 = 8.1, 81 ÷ 100 = 0.81   

Your number line example with 8 highlighted:

 

Number sentence (equation) example:

81 + 5 = 86

639

six-hundred and thirty-nine; 

odd; 

half it = 319.5; 

double it = 1,278; 

hundreds = 6, tens = 3, ones = 9; 

10 less = 629, 10 more = 649, 100 less = 539, 100 more = 739; 

add 15 = 654, subtract 7 = 632, multiply by 6 = 3,834 (I used the columns strategy), divide by 3 = 213 (I used long division); 

639 x 10 = 6,390; 639 x 100 = 63,900; 639 ÷ 10 = 63.9, 639 ÷ 100 = 6.39   

Your number line example with 639 highlighted:

 

Number sentence (equation) example:

639 + 5 = 644

3,490

three-thousand, four-hundred and ninety; 

even; 

half it = 1,745; 

double it = 6,980; 

thousands = 6, hundreds = 4, tens = 9, ones = 0; 

10 less = 3,480, 10 more = 3,500, 100 less = 3,390, 100 more = 3,590; 

add 15 = 3,505; subtract 7 = 3,483; multiply by 6 = 20,940 (I used the columns strategy), divide by 3 = 1,163 R1 (I used long division); 

3,490 x 10 = 34,900; 3,490 x 100 = 349,000; 3,490 ÷ 10 = 349; 3,490 ÷ 100 = 34.9   

Your number line example with 3,490 highlighted:

Number sentence (equation) example:

3,490 + 5 = 3,495

76,200

seventy-six-thousand, two-hundred; 

even; 

half it = 38,100; 

double it = 152,400; 

thousands = 76, hundreds = 2, tens = 0, ones = 0; 

10 less = 76,190, 10 more = 76,210, 100 less = 76,100, 100 more = 76,300; 

add 15 = 76,215; subtract 7 = 76,193; multiply by 6 = 457,200 (I used the columns strategy), divide by 3 = 25,400 (I used long division); 

76,200 x 10 = 762,000; 76,200 x 100 = 7,620,000; 76,200 ÷ 10 = 7,620; 76,200 ÷ 100 = 762   

Your number line example with 76,200 highlighted:

Number sentence (equation) example:

76,200 + 5 = 76,205

Monday, August 23

10

ten; 

even; 

half it = 5; 

double it = 20; 

tens = 1, ones = 0; 

10 less = 0, 10 more = 20, 100 less = -90, 100 more = 110; 

add 15 = 25, subtract 7 = 3, multiply by 6 = 60, divide by 3 = 3 R1; 

10 x 10 = 100, 10 x 100 = 1,000, 10 ÷ 10 = 10, 10 ÷ 100 = 0.1   

Your number line example with 10 highlighted:

 

Number sentence (equation) example:

10 + 5 = 15

67

sixty-seven; 

odd; 

half it = 33.5; 

double it = 134; 

tens = 6, ones = 7; 

10 less = 57, 10 more = 77, 100 less = -33, 100 more = 167; 

add 15 = 82, subtract 7 = 60, multiply by 6 = 402, divide by 3 = 22 R1; 

67 x 10 = 670, 67 x 100 = 6700, 67 ÷ 10 = 6.7, 67 ÷ 100 = 0.67   

Your number line example with 8 highlighted:

 

Number sentence (equation) example:

67 + 5 = 72

928

nine-hundred and twenty-eight; 

even; 

half it = 464; 

double it = 1,856; 

hundreds = 9, tens = 2, ones = 8; 

10 less = 918, 10 more = 938, 100 less = 828, 100 more = 1,028; 

add 15 = 943, subtract 7 = 921, multiply by 6 = 5,568 (I used the columns strategy), divide by 3 = 309 R1 (I used long division); 

928 x 10 = 9,280, 928 x 100 = 92,800, 928 ÷ 10 = 92.8, 928 ÷ 100 = 9.28   

Your number line example with 928 highlighted:

 

Number sentence (equation) example:

928 + 5 = 933

4,632

four-thousand, six-hundred and thirty-two; 

even; 

half it = 2,316; 

double it = 9,264; 

thousands = 4, hundreds = 6, tens = 3, ones = 2; 

10 less = 4,622, 10 more = 4,642, 100 less = 4,532, 100 more = 4,732; 

add 15 = 4,647, subtract 7 = 4,625, multiply by 6 = 27,792 (I used the columns strategy), divide by 3 = 1,544 (I used long division); 

4,632 x 10 = 46,320, 4,632 x 100 = 463,200, 4,632 ÷ 10 = 463.2, 4,632 ÷ 100 = 46.32   

Your number line example with 4,632 highlighted:

Number sentence (equation) example:

4,632 + 5 = 4,637